[ad_1]
We are made use of to studying stories professing that a study was completed, and the individuals showed the impact. The contributors in the experimental group outperformed all those in the regulate group. Frequently the report provides that the impact was statistically significant, possibly at the .05 stage or even at the .01 degree.
So it is easy to form the perception that all the members showed the influence. Nevertheless, that would be erroneous.
In assessments of statistical significance, p-values (and impact measurements) are effectively the distinction among group indicates divided by (or expressed in phrases of) the common deviation. Statistical importance is with regard to group averages. So to what extent does a variance between group means stand for the discrepancies involving individuals?
Possibly the individuals all showed the consequence, but only to a incredibly small extent, and the significant selection was sufficient to generate statistical significance. Statisticians have concerned about this probability and have invented steps of impact dimensions to clarify the discovering. Sad to say, couple reports, in particular in the media, include things like any information about result size—probably because when you insert a lot more information like this, you just muddy the photograph and confuse the reader.
Perhaps only some of the participants showed the result, but showed it to a substantial extent, balancing out all those who didn’t present any effect at all. Very simple measures of variability will display if this may possibly be the case, but once again, several lay viewers will not recognize or be interested in the indicating of variability and most of the experiences they receive will not involve normal deviations.
So let’s try out a further approach—making it really straightforward for readers to grasp how pervasive an influence is.
To explore this problem, we received knowledge from an actual funded analyze (not performed by us) comparing two groups in phrases of effectiveness at a job that was possibly aided by an AI procedure (experimental team) or not aided by an AI method. There were being 30 participants in each team, a fair amount. This particular details established was picked since the distributions seem to be about standard (working with the “eyeball” take a look at).
You can see the final results beneath. The distribution for the experimental situation is shown in blue and the distribution for the management problem is demonstrated in orange. The figure reveals that the two distributions overlap a superior deal.
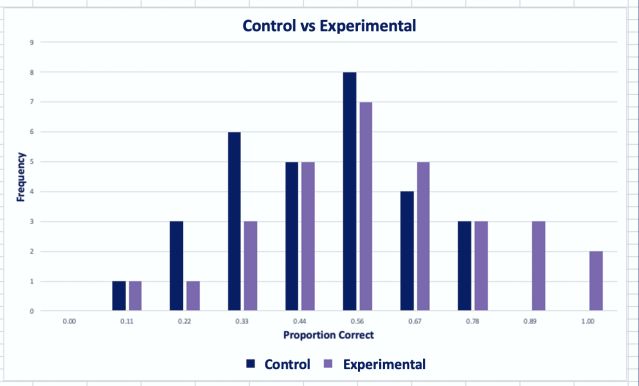
Overlapping Distributions for Experimental and Regulate Teams.
Resource: Robert Hoffman
So there’s an outcome right here, and it is statistically significant: p<,001, using a two-tailed t-test. But it certainly isn’t universal. We need to keep that in mind when we discuss findings such as these.
But what would it take to make this significant effect at the p<.001 level disappear?
The Peelback Method
We can progressively peel away the extremes. First, we removed the data for the two participants in the experimental group who scored the highest and the one participant in the control group who scored the lowest.
Bingo.
The proportion of correct responses in the experimental group dropped from 65% to 54%, and the proportion correct in the control group increased a little, from 48% to 49%, and now the t-test shows p<.334. Not even close to being counted as statistically significant. So the initial “effect” doesn’t seem very robust.
If the statistical significance were still achieved after this first peel, we could keep peeling and recomputing until the p<.05 level was crossed. We might find that we had to do a lot of peeling. In that case, we would have much more confidence in the conclusion about the statistical significance. But if statistical significance disappears merely by dropping three of the 60 participants, then how seriously can we take the results? Or how seriously should we take the t-test?
This general method could be turned into an actual proportional “metric,” that is, the number of “peeling steps” relative to the total sample size. In the present case, that number is 3/60. The smaller that number, the more tenuous the statistical effect.
Side note: We did not cherry-pick this example. We simply wanted a simple data set that yielded statistically significant results. We had no idea in advance that the example would illustrate our thesis so well.
Conclusion
For lay readers of psychology research reports, the peelback method might be much easier to grasp than other kinds of statistics such as effect sizes.
Researchers themselves might find it a useful exercise to explore and examine the peelback method for their own experiments. If they have the courage. Researchers could then consider which participants were responsible for the findings and what these participants were like.
But let’s think again about what the peeling entails. Some statistics textbooks refer to the problem of “outliers,” and even present procedures enabling researchers to justify the removal of data from outliers. The concept seems to be that “outliers” just add noise to the data, hiding the “true” effects.
The highest-performing participants in an experimental group (in studies like the one referenced here) demonstrate what is humanly possible. The worst-performing participants in both the experimental and the control groups might be pointers to issues of motivation or selection. The “best” and the “worst” performers are the individuals who should be studied in greater detail say, by in-depth post-experimental cognitive interviews.
Unfortunately, many psychological studies do not include in-depth post-experimental cognitive interviews as a key part of their method, and even when interviews are conducted, the results are usually given short shrift in the research reports. Data about what people are thinking will always clarify the meaning and “significance” of the numerical results.
So this little exploration of a simple idea exposes some substantive issues and traps in research methodology. Not the least of these is a cautionary tale, to never confuse a statistical effect (about groups) with a causal effect an independent variable might have on individuals.
Robert Hoffman is a co-author for this post.
[ad_2]
Source link
